1. Hình chóp tứ giác đều có tâm đối xứng không?
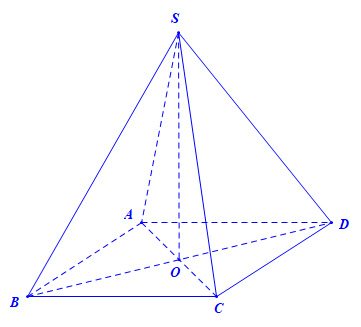
Hình chóp tứ giác đều không có tâm đối xứng. Một hình chóp tứ giác đều là một hình chiếu của một hình tứ giác đều trên mặt phẳng cơ sở, và các cạnh của hình chóp tứ giác đều không cùng chiều dài. Do đó, không có điểm nào trong hình chóp tứ giác đều có thể làm tâm đối xứng.
2. Tâm đối xứng của hình chóp tứ giác đều là điểm nào?
Hình chóp tứ giác đều không có tâm đối xứng.
3. Tại sao hình chóp tứ giác đều có tâm đối xứng?
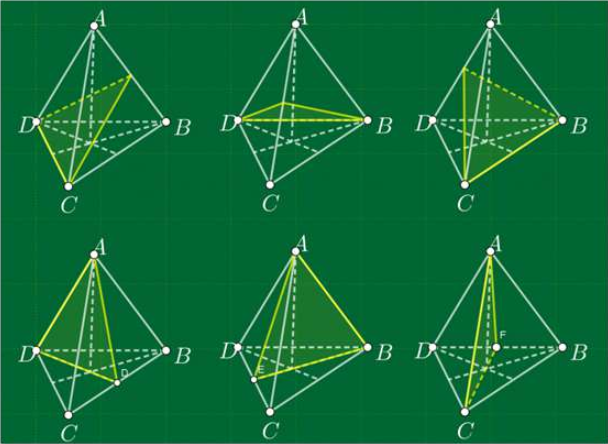
Vì hình chóp tứ giác đã được quay quanh một trục thông qua tạo thành các giao diện vuông góc với mặt phẳng cơ sở, các bán kính từ trục này để lại các điểm trung bình cho tất cả các cạnh của nhiệm vụ.
4. Cách tính toán tìm tâm đối xứng của hình chóp tứ giác đều là gì?
Không có công thức cụ thể để tính toán tâm đối xứng của hình chóp tứ giác đều vì nó không tồn tại.
5. Liên quan giữa tâm đối xứng và tính chất của hình chóp tứ giác đều là gì?
Vì hình chóp tứ giác đều không có tâm đối xứng, nên không có tính chất nào liên quan trực tiếp đến tâm đối xứng trong trường hợp này. Tuy nhiên, các tính chất khác của hình chóp tứ giác đều bao gồm cạnh bằng nhau và các mặt bằng nhau, góc giữa hai mặt phẳng cơ sở là vuông góc, và các giao diện từ trung điểm của các cạnh cơ sở để lại các điểm trung bình cho các cạnh bên.
Kết luận, hình chóp tứ giác đều không có tâm đối xứng. Hình chóp tứ giác đều không thể có tâm đối xứng vì trọng tâm của mặt phẳng đáy và các cạnh bên không trùng nhau. Điều này nghĩa là không thể tìm được một điểm duy nhất để quay hình chóp tứ giác đều thành một hình chóp tứ giác mới thông qua quá trình quay. Do đó, hình chóp tứ giác đều không có tâm đối xứng.