1. Hình chóp tứ giác đều có tất cả 8 cạnh. Bởi vì hình chóp tứ giác có 4 cạnh bên và 4 cạnh đáy, do đó có tổng cộng 8 cạnh.
2. Lý do hình chóp tứ giác đều có 8 cạnh là vì nó được tạo thành từ một đáy là một tứ giác và các cạnh kết nối từ các điểm trên đáy lên đỉnh của hình chóp. Với mỗi điểm trên đáy, ta có thể kết nối với các điểm khác để tạo thành 4 cạnh bên của hình chóp. Tổng số các cạnh bên là 4×2=8.
3. Công thức tính số cạnh của một hình chóp n-giác là 2n, trong đó n là số cạnh của đa diện đáy. Ví dụ, nếu hình chóp có một đa diện đáy là tam giác (3-giác), thì số cạnh của hình chóp sẽ là 2×3=6.
4. Hình chóp tứ giác chỉ có duy nhất một mặt phẳng đáy, và không có mặt phẳng đáy khác.
5. Để xác định các mặt phẳng đối xứng trong hình chóp tứ giác đều, ta có thể sử dụng các công thức và quy tắc của hình học. Một số phương pháp xác định mặt phẳng đối xứng là sử dụng các trục đối xứng của hình chóp, kiểm tra tính chất đối xứng của các điểm trong hình chóp, hoặc sử dụng các công thức và quy tắc về mặt phẳng đối xứng.
1. Số mặt phẳng đối xứng của hình chóp tứ giác đều là bao nhiêu?

Hình chóp tứ giác đều có tất cả 4 mặt phẳng đối xứng. Mỗi mặt phẳng đối xứng là một mặt phẳng đi qua cạnh bên của hình chóp và đi qua tâm của đáy. Do đó, số mặt phẳng đối xứng của hình chóp tứ giác đều là 4.
2. Tại sao hình chóp tứ giác đều có 8 cạnh?
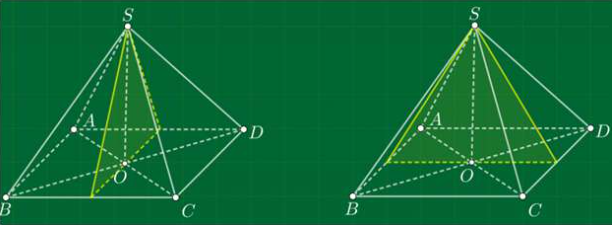
Hình chóp tứ giác (ví dụ như hình vẽ trên) có 4 cạnh bên và 4 cạnh đáy nên có tất cả 8 cạnh.
Chú ý: Chóp n – giác có 2n cạnh.
3. Công thức tính số cạnh của một hình chóp n-giác là gì?
Công thức tính số cạnh của một hình chóp n-giác là 2n, trong đó n là số cạnh của đa giác đáy.
Ví dụ: Nếu hình chóp có một tam giác làm đáy, thì số cạnh của hình chóp sẽ là 6 (2 x 3).
4. Hình chóp tứ giác có bao nhiêu mặt phẳng đáy?
Hình chóp tứ giác có một mặt phẳng đáy duy nhất. Mặt phẳng đáy là một tứ giác và tạo thành cạnh đáy của hình chóp.
5. Làm thế nào để xác định các mặt phẳng đối xứng trong hình chóp tứ giác đều?
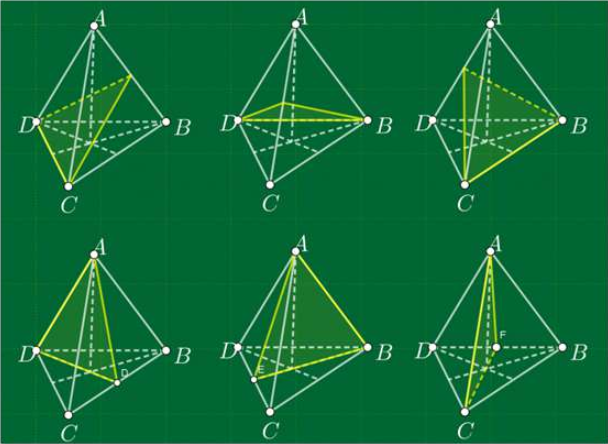
Để xác định các mặt phẳng đối xứng trong hình chóp tứ giác đều, ta cần tìm các trục đối xứng của hình. Mỗi trục đối xứng là một đường thẳng đi qua tâm của hình chóp và song song với cạnh bên của nó. Các mặt phẳng đi qua các cạnh bên và trung tâm dọc theo các trục này sẽ là các mặt phẳng đối xứng của hình chóp tứ giác đều.
Trên thực tế, một hình chóp tứ giác đều có tổng cộng 4 mặt phẳng đối xứng. Điều này được chứng minh bằng cách quan sát các đối xứng của hình chóp tứ giác đều trong không gian ba chiều. Bốn mặt phẳng đối xứng này giúp tạo nên tính đẹp và cân bằng cho hình chóp tứ giác, làm nổi bật những đặc điểm hình học của nó.